The auroral zone conductances can be estimated from the energy flux and
average energy of precipitating electrons. The DMSP satellite measures the
electron spectral distribution as described in section 4.1 and these measurements
can be converted, using several methods, into conductances of the E-layer.
A simple expression relating the energy flux and the average energy of the
electrons with the height-integrated Hall and Pedersen conductances was
described by Robinson et al. [RVM 
87]. The approach makes
the assumption that the conductances produced by an actual electron energy
distribution can be approximated by those produced by particles with a
Maxwellian energy distribution having the same energy flux and average energy.
The average energy of precipitating particles 
is computed
according to
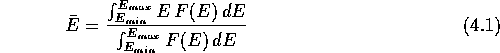
where 
and 
are the minimum and maximum energies measured
by the detector and F(E) is the differential electron flux. In practice
the calculation is performed on the discrete energy channels using the
trapezoidal rule for numeric integration. With this
average energy and the energy flux 
of the electrons the
following expressions can be used to determine the Hall conductance
and Pedersen conductance 
:
where is measured in keV, in 
,
and in mhos. A
correction factor of up to 2.0 has to be applied for large average energies
when the spectrum is measured below an energy level that is comparable to
the average energy. Also has to be chosen sufficiently high for the
assumption of a Maxwellian distribution to hold; 
is a good
limit for terminating the integration. Comparisons have shown that these
estimations yield conductivities that are within 25% of the actual values
for most common types of auroral energy distributions
[RVM 87, p. 2568,]. It is also important
to note that averaged auroral conductivity estimates have a much smaller
magnitude since they are despiked by the averaging process. Also, for actual
conductivity values one
has to take the conductivity produced by solar radiation into account. This
depends on the level of solar power flux at 
, denoted by 
, and the solar
elevation angle 
. The solar radiation conductivity contributions
are estimated by Hardy et al. [HGRM87] to be:
Since the spatial variation of the conductivity produced by the solar
radiation is small for SuperDARN target area sizes and therefore of little
importance for this work, these conductivities are not considered for
the data analysis [HGRM87]. There is also evidence that the
conductances resulting from photoionization can not be easily modeled using
the solar zenith angle and the solar 10.7cm radio flux as scaling
parameters. At zenith angles of 
the solar radiation components of
the Pedersen and Hall conductances are systematically overestimated
[WdN92].
The ions have not been taken into account in the conductivity calculations. This is justified in most cases, since in general the ion flux is two orders of magnitude lower than the electron flux. Furthermore, there exist no simple models to include the ion precipitation in conductivity models, while existing complex models which do account for ions have to be refined and checked experimentally [BJSD93].