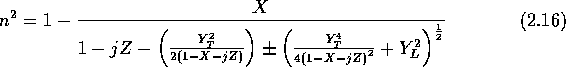
Since this thesis concerns radar studies of the F-region, it is useful to establish the background theory for radiowave propagation in a uniform magnetoplasma, known as magneto-ionic theory. Its cornerstone is the formula for the refractive index of an ionized medium in a magnetic field. The form that is now generally used resulted from the work of E. V. Appleton between 1927 and 1932 and is called the Appleton-Hartree equation. The complex refractive index n appropriate for E- and F-region studies is defined by the following equation:
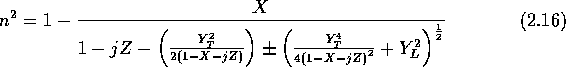
where the dimensionless quantities X, Y and Z are defined as follows:
where 
is the angular plasma frequency,
is the electron gyro-frequency,
is the angle between the propagation direction and the geomagnetic
field, 
is the electron collision frequency and 
is the angular
wave frequency [Har92, pp. 25-26,].
Two special cases of this equation are often used, namely the
quasi-longitudinal (QL, propagation roughly parallel to 
)
and the quasi-transverse (QT, propagation roughly perpendicular to )
approximations. At high frequencies, that is when 
8
MHz, the collisional term Z may be neglected. The refractive index is then
purely real or imaginary.
For quasi-transverse propagation ( 
and 
), the Appleton-Hartree equation
reduces to the following forms for the upper and lower sign respectively:
The wave mode which is unaffected by the magnetic field defined by
is called the ordinary mode. The refractive index for the
extraordinary wave 
has cutoffs ( 
)
for X = 1 + Y and X = 1 -Y, and a resonance for 
.
For quasi-longitudinal propagation ( 
and 
), the Appleton-Hartree equation reduces to:
The importance of this case comes from the fact that the
propagation at frequencies above 8 MHz is quasi-longitudinal as long as
the angle is less than 
or more than 
.
Very important to analysis of SuperDARN data is the behavior of the horizontal
linear transmitted waves in the plasma in the presence of a magnetic field.
When such a horizontal linearly polarized wave reaches the ionosphere, it splits into two circular waves
whose electric vectors are in phase at the horizontal position but which
are rotating in opposite directions. Because the refractive index differs
for the two circular components, an increasing phase difference between them
along the propagation path will occur. As a result, the major axis of the
polarization ellipse of the radiowave, formed from the sum of the two
circular components, will rotate by half the phase difference between
the components. The major axis rotation is called Faraday rotation and
is derived from the expression for the electric field. The refractive index
is expressed as a complex number with the components 
and 
:
The electric field vibrations will then be of the form:
where the second factor defines the phase. The Faraday rotation 
is given by
where f is the radio wave frequency in Hz ( the corresponding
angular frequency), 
the longitudinal component of the magnetic
field in T and N is the electron density, both along the raypath to the
reflector. This is an important consideration for SuperDARN measurements
since the wave might be rotated by 
once it reaches the
receiver, i.e. at right angles to the antenna polarization, producing a
complete loss of signal. Also, since the scattered power from the left circular
(ordinary) and right circular (extraordinary) received waves is different
a further change in the polarization state of the wave vector occurs.
Thus, the power of the returned
radio backscatter as measured by the horizontally polarized antennas of the
SuperDARN radar is generally less than the actual power in the scattered
signal [Sof68, Appendix C,].
