The gradient drift instability [Sim63, Hoh63]
is a relative of the Rayleigh-Taylor instability,
since they both involve the interchange of two elements of a fluid plasma. It
is also known as the `` 
'' or cross-field instability.
If an enhancement of the plasma density is present whenever an external force
acts on the same volume of plasma (due to an electric field, gravity or
neutral air winds) and a slight disturbance occurs, a charge separation can
take place. This charge separation produces a small ``polarization electric
field'' which, due to the presence of a magnetic field,
increases the disturbance, thus producing the instability. This instability
is a common mechanism by which irregular structures in the F-region break
down into smaller ones [Har92, p. 41,].
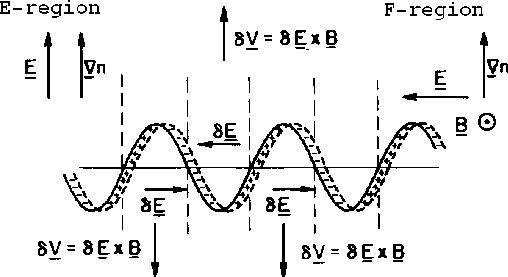
Figure 2.6: The gradient drift instability and 
and 
conditions for instability growth in the E-region (left) and the F-region
(right).
Shown in Figure 2.6 is a diagram that outlines the
gradient-drift mechanism. If the electric field
is parallel to the plasma density gradient , the condition for
instability growth in the E-region is met. The electrons and ions will have
different drift velocities and directions, creating a charge separation
along an initial disturbance as indicated. The electrons will move
perpendicular to the electric field with a speed 
(collisionless Hall drift) while the ions move along the direction of the
electric field with a speed of 
(Pedersen drift).
The resulting polarization electric field
will produce a 
drift which
drives the amplitude increase of the instability.
The same charge configuration holds for
the F-region, but the condition is now that the electric field
is perpendicular to the plasma density gradient . The collision
frequency for electrons and ions is low at these altitudes, resulting in a
collisionless Hall drift of both electrons and ions. The charge separation
is produced through the large Pedersen mobility of the ions as compared to
that of electrons. The Pedersen drift component of the ions is directed
along the electric field.
There exist several mechanisms which have an influence on the growth
rate of this instability at high latitudes.
If the E-region is highly conductive, as is often the case in auroral regions, the
perturbation charges of the F-region may be shorted out by a current flow to the
E-region, so
the growth rate of the gradient-drift instability becomes small.
In addition to these structure related
currents, large-scale field-aligned currents can be present.
In such cases, if the propagation vector 
has a small component
along the magnetic field, the relative velocities between the
ions and electrons along the FAC will have a component along . This
will in turn lead to polarization fields that support the growth of the
initial perturbed wave. This is called the current
convective instability [OC79, Kad65]. Its importance
relative to the gradient-drift instability is formed from the
ratio of the growth rates 
for the basic gradient
drift and the current convective mechanisms:
It should be noted that the above results are based on linear theory. This has a major shortcoming, since the growth rates are rapid, particularly for the current convective instability, and the instability can quickly become nonlinear [Cha79, KOC80]. Still, the current convective instability appears to explain the observations of ionospheric F-region irregularities when density gradients and FACs are present [Kel89, p. 369 - 377,].