Multipulse

With multi-pulse techniques, one seeks to transmit a pattern of pulses such that the pulse separations contain most or all of the lags necessary for determining the ACF and such that there is little or no ambiguity in the ranges that contribute to any given lag. This technique is considerably more efficient than the variable-lag double-pulse technique from an analysis point of view; it requires far less time. Some minor problems with the technique are the presence of increased noise background due to uncorrelated scatter and the occurrence of missing samples when the transmitter is operating during sampling [BG 88, GBV83]. Figure 3.5 shows the details of sequencing and ACF generation for different lags of a pulse sequence that will be presented later in Table 3.3.

  
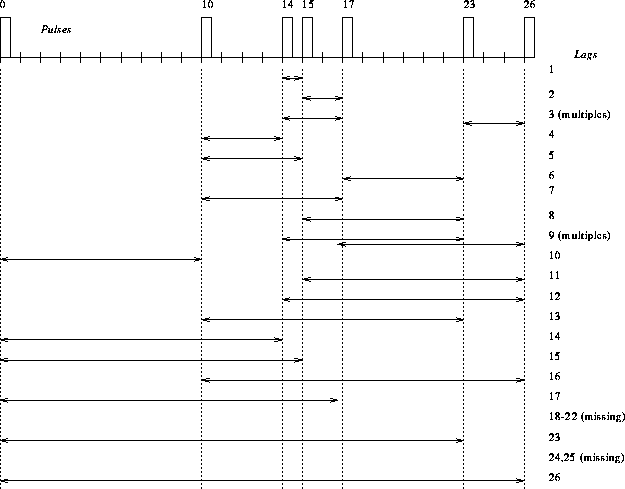
Figure 3.5: Pulse combinations to generate 17 usable lags from a 7 pulse sequence

As can be seen, many combinations are possible. Several lags are not usable because they are either missing or ambiguous. Lags become ambiguous if they occur more than once within the sequence. If the two pulses are separated by a lag time t and scattering occurs at two ranges separated by a distance , the signals from these two target regions would arrive back at the same time (pulse 1 from the range and pulse 2 from the range R), so a resolution of these ranges would not be possible. If on the other hand this time t corresponds to a distance that is larger than the extent of the scattering region, the multiple pulse-pattern can be used. An important feature is the long separation of the first pulse from the other pulses. The reason is that the determination of the scattering intensity is based upon the zero-lag value of the ACF, which requires essentially a single pulse. Therefore an optimum pulse sequence has to meet several requirements which are listed below.

• The pulse sequence should have a long maximum-lag for a given number of pulses.
• The pulse sequence should have as few missing lags as possible.
• The pulse sequence should have as few multiple (or ambiguous) lags as possible.
• The pulse sequence should have one pulse separated well from the others.

The pulse sequence presented in Figure 3.5 is not the only one and by far not the best one possible. The generation of new pulse sequences can be accomplished easily with a simple computer program using a ``brute-force'' method that generates and tests simply all possible sequences. Its functional steps can be summarized as follows.

1. Define the number of pulses and the maximum separation in time of two consecutive pulses M, in units of the basic lag time T.
2. Define some limits for the run. For example set the minimum on the longest lag from the sequence, the maximum number of missing lags and the maximum number of multiple lags for the sequence to be considered `good'.
3. Permutate pulse separations up to a maximum separation of M. This generates all possible pulse sequences.
4. Analyze the pulse sequence calculating the number of missing and multiple lags and the maximum separation of a single pulse in the sequence.
5. Determine the quality of the sequence according to the limits from step 2 and generate output if it satisfies the criteria.
6. Go to step 3 if there are sequences left; check this using a counter.

For example the input of and M=2 would generate sequences which are: (0,1,2),(0,1,3),(0,2,3) and (0,2,4). A typical run of the optimized C-program on a personal computer (486DX2-66) takes between 10 minutes to 24 hours to complete depending on the values of and M. Table 3.3 lists some possible pulse sequences from the computer analysis, using the above algorithm. The number of ``good'' lags in the table is equivalent to the number of ACF data points that can be generated, including the lag-0 value. Not all requirements for a good multipulse sequence are always met by these examples, but they provide some very efficient sequencing possibilities.

  
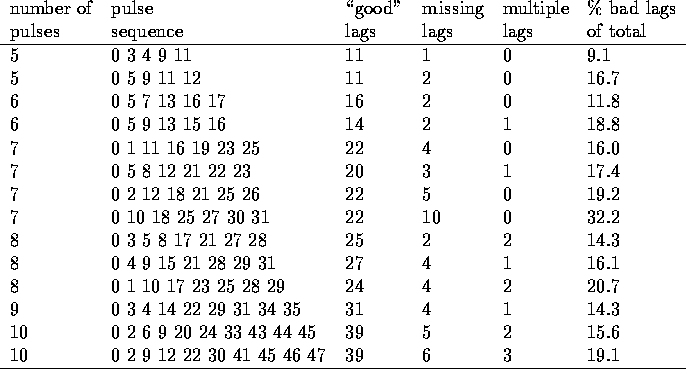
Table 3.3: Examples of optimized multi-pulse patterns