The autocovariance function is the basis for the determination of the Doppler velocity power spectrum of the scattering region or equivalently, assuming that only a single velocity component is present, the determination of the mean Doppler velocity of the scatterers.
To determine the complex ACF values at a specific lag-time, two
pulses that are separated by a time interval 
are considered
. Since
the analysis that follows deals with proportional values only, constants
have been dropped. As shown in Section 3.1, voltages at
the receiver depend
on the Fourier component of the density fluctuation with wave vector
(or 
in short). Therefore the voltages of
the two measurements are (see Figure 3.4):
where 
is a variable of integration and 
is the frequency
of the radar wave.
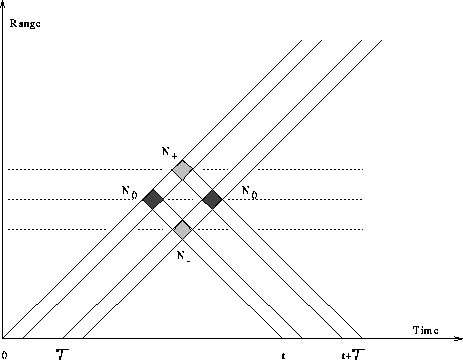
Figure 3.4: Range-time diagram for two pulses seperated by a time
The backscattered signal from two pulses can contain the three components
, 
and 
as indicated in Figure 3.4.
.
The received voltages can be mixed with two phase-coherent transmitted
frequency components that differ by 
in their phase. As an example
the voltage measurements at time t are described in
Equation 3.36 and 3.37. The
voltages at time are derived the same way. These voltages are taken
to be different and correspond to the real and imaginary component of the
signal.
Low-pass filtering
can then be used to remove the HF part corresponding to a frequency of
. We are left with the two voltages 
and
, one corresponding to the real and one to the imaginary component
of the complex voltage measurement 
:
The voltages are averaged over several measurements. We denote the
averaging process by 
. Furthermore a ratio between two voltages
differing by the lag time , that is
and 
, is formed.
Using the following short-hand notation for the electron density spectra
the ratio of the two time separated and averaged voltage measurements can be expanded and written as follows:
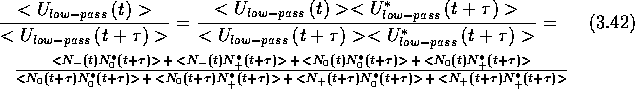
where * denotes a complex conjugate value. The information about the Doppler
shift is contained in the term 
. It is not
possible to determine this term by a single measurement since all terms in the
above ratio are of the same order. But since we are dealing with averaged
values uncorrelated values will go to zero in the mean. Thus, we assume that
the mean values of the received voltages are zero, and the densities
, and are independent.
The term defining the ACF of the power spectrum belonging to at lag
, that is 
, is then separable easily
from the ratio [And80, p. 11-15,]. To determine a complete ACF as a
function of , this procedure has to be repeated for different .
