Noether’s Theorem is a central result in theoretical physics that expresses the one-to-one correspondence between symmetries and the conservation laws.
My daughter wrote about Emmy Noether and her impact on mathematics and physics for a school project. as we found out together, the theorem is kind of hard to explain. Here is my attempt to break down the above statements into some key parts and describe them seperately. Maybe this is of help to others!
How does a Physisist use this theorem?
One can use the theorem in two ways:
- If on observes some kind of symmetry (i.e. in location), there must be a conservation law (i.e. conservation of linear momentum).
- If one observes some kind of conservation law (i.e. conservation of energy), there must be a symmetry (i.e. time independence).
So why do we care?
Noether’s theorem is an amazing result which lets physicists get conserved quantities from symmetries of the laws of nature, i.e. it is a tool for physicists: it makes new discoveries and progress in Physics possible just like Galileo’s telescope made it possible to observe Mars, or Einstein’s theory of relativity made it possible to build an A-bomb.
What is theoretical physics?
That is easy to explain by contrasting the activities of theoritical physics with the ones done in experimental physics.
Experimental Physics: example the LHC
- Experiment
- Measurements
- Cables, electronics, computers
- “Machines that do stuff”
Theoretical Physics: example supersymmetry
- Blackboards, Paper
- Formulas, Math
- Graphs, Diagrams
- Models
What is one-to-one correspondence?
Example: identical twins
Each twin can be said to have a one-to-one correspondence in genetic makup with the other twin.
In math, this is also called Bijection.
What is symmetry?
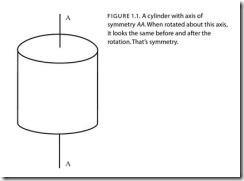
Quote: “… when rotated about the axis, it looks the same as before and after the rotation. That’s symmetry.”
What are conservation laws?
In Physics: conservation == some physical property is the same before and after some change
The most important examples of conservation laws are the following:
- the energy is conserved if and only if (iff) the physical laws are invariant under time translations (if their form does not depend on time).
In this example, the army general does not have to worry about when to fire the bullet when considering the trajectory of the projectile (, but the general does still have to worry about other physical properties that might affect the trajectory such as wind, temperature, angle of the turret, amount of gunpoweder, etc.).
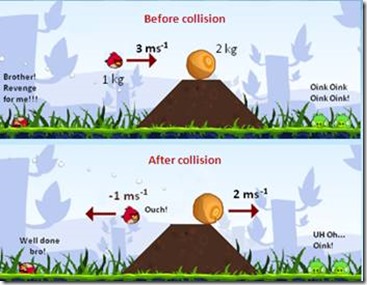
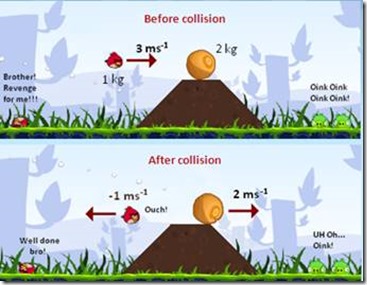
- the linear momentum is conserved iff the physical laws are invariant under spatial translations (if the laws do not depend on the position)
On Earth
On the Moon
The spatial translation in this example is the act of flying to the moon with a rocket. So if our austronaut where to be playing “Angry Birds” first on the Earth and then on the Moon, she would observe the same linear recoil (, but since the gravity on the moon is lower, the trajectories and bounce effects would be vastly different of course).
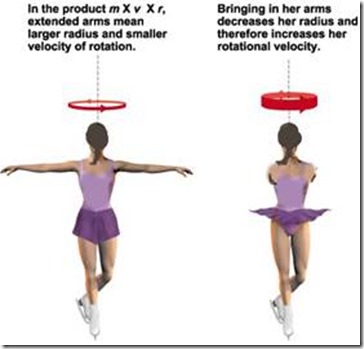
- the angular momentum is conserved iff the physical laws are invariant under rotations (if the laws do not care about the orientation)
From the front:
From the back:
The dancer pulls in her arms, and she will spin faster making for a great audience effect. This will work the same way independent of the position on the rink or the direction the is looking when she starts pulling in her arms; Similarly, the audience will see this effect regardless where they sit in the stadium, even when looking at the dancer from the back.






![clip_image010[1] clip_image010[1]](http://www.ferzkopp.net/wordpress/wp-content/uploads/2016/01/clip_image0101_thumb.png)